Preguntas frecuentes
¿Qué es y para qué sirve un diagrama de dispersión?
¿Cómo se hace un diagrama de dispersión?
1. Recopilar datos: Obtén pares de valores para las dos variables que quieres analizar.
2. Dibujar ejes: Traza un eje horizontal (X) para una variable y un eje vertical (Y) para la otra.
3. Escalar ejes: Divide los ejes en intervalos adecuados según los valores de tus datos.
4. Marcar puntos: Para cada par de valores, ubica un punto en la gráfica, con su valor en X en el eje horizontal y su valor en Y en el eje vertical.
5. Interpretar: Observa la distribución de los puntos para identificar patrones, tendencias y posibles correlaciones entre las variables.
¿Cómo explicar un diagrama de dispersión?
¿Qué es un gráfico de dispersión en Excel?
Un gráfico de dispersión en Excel es una herramienta visual que muestra la relación entre dos conjuntos de datos numéricos. Cada conjunto de datos se representa como un punto en el gráfico, con una variable en el eje X y la otra en el eje Y. Esto permite identificar patrones, tendencias o correlaciones entre las variables, lo que facilita el análisis y la toma de decisiones.
¿Cómo hago un diagrama de dispersión en Excel?
Para hacer un diagrama de dispersión en Excel, sigue estos pasos:
- Organiza tus datos: Asegúrate de tener dos columnas de datos numéricos que quieras comparar.
- Selecciona los datos: Resalta ambas columnas de datos.
- Inserta el gráfico: Ve a la pestaña «Insertar» y en la sección «Gráficos», elige el icono de «Dispersión» (puntos). Selecciona el subtipo de gráfico de dispersión que prefieras.
- Personaliza el gráfico: Agrega títulos a los ejes, un título al gráfico y cualquier otro elemento de formato que desees.
El diagrama de dispersión es una herramienta utilizada cuando se desea realizar un análisis gráfico de datos bivariados, es decir, los que se refieren a dos conjuntos de datos.
En un proceso de manufactura, siempre existirán un número de factores que impactan a los resultados deseados.
Para que un producto sea de calidad, debe cumplir con todas las especificaciones y requerimientos no solamente dimensionales, sino también de sus propiedades y características, por ejemplo, resistencia, desempeño, e incluso apariencia.
Estas funciones, que conocemos como “entregables” pueden considerarse como variables respuesta de un conjunto de otras variables que son las que las causan. Si tenemos parámetros establecidos de un proceso, sabemos por experiencia dentro de que rangos nos podemos mover. Si conocemos el comportamiento de nuestro producto, tal vez pensemos que es suficiente simplemente mantenernos dentro de los márgenes conocidos. Pero siempre hay aspectos que no conocemos del todo, o que asumimos conocer.
Si empezamos a hacer diagramas que representen dichos comportamientos de nuestras variables de proceso en base a datos obtenidos del mismo, la herramienta más práctica a utilizar es el diagrama de dispersión.
¿Qué es un Diagrama de Dispersión?
El diagrama de dispersión es una herramienta utilizada cuando se desea realizar un análisis gráfico de datos bivariados, es decir, los que se refieren a dos conjuntos de datos. El resultado del análisis en el diagrama puede mostrar que existe una relación entre una variable y la otra.
El diagrama de dispersión tiene el propósito de controlar mejor el proceso y mejorarlo, resulta indispensable conocer cómo se comportan algunas variables o características de calidad entre sí, esto es, descubrir si el comportamiento de unas depende del comportamiento de otras, o no, y en qué grado.
Se le llama diagrama de dispersión, porque al momento de graficar los puntos de coincidencia de cada variable con respecto a la otra, estos puntos se van dispersando o posicionando en el diagrama de acuerdo con el grado de relación entre ambas.
El estudio puede ampliarse para incluir una medida cuantitativa de tal relación.
Estas dos variables del diagrama pueden ser:
-
- Una característica de calidad y un factor que incide sobre ella
- Dos características de calidad relacionadas
- Dos factores relacionados con una misma característica de calidad
¿Para qué sirve un diagrama de dispersión?
-
- El diagrama de dispersión nos indica si dos variables (o factores o características de calidad) están relacionados
- El diagrama de dispersión además puede proporcionar la posibilidad de reconocer fácilmente relaciones causa/efecto
¿Cómo se construye el diagrama de dispersión?
Paso 1: Definir las variables a diagramar en el diagrama
Para nuestro ejemplo usaremos el tiempo del proceso en segundos y el espesor del producto resultante en milímetros.
Paso 2: Determinar escalas para las variables del diagrama
Diseñar las escalas apropiadas para los ejes X y Y. Si vamos a realizar el diagrama en una hoja o carta de papel, hay que ver en que rangos de cada variable nos vamos a mover (su mínimo y su máximo) para que tracemos la escala y en ella indicar los valores que vamos a estar midiendo.
Podemos realizar la gráfica en Excel o en Minitab y si es así, el software nos podrá generar en forma automática estas escalas.
Paso 3: Recolectar los datos del diagrama
Procedemos a realizar las mediciones durante el proceso de interés.
Recolectar “n” parejas de datos de la forma (Xi, Yi), con i = 1, 2, 3,… “n” donde Xi y Yi representan los valores respectivos de las dos variables. Para nuestro ejemplo sería para cada tiempo progresivamente medir y anotar el espesor que resulta.
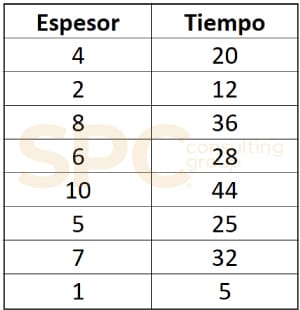
Paso 4: Generar el diagrama
Trazar los puntos en nuestra hoja de diagrama de dispersión, o bien graficarlos en el software deseado. En nuestro ejemplo vemos que existe una correlación entre ambas variables, a mayor tiempo mayor espesor.

Paso 5: Lectura y uso del Diagrama de Dispersión
En un diagrama de dispersión el patrón de puntos puede asumir formas diversas, dependiendo de la relación que exista entre las variables. Si el patrón de puntos asume la forma (quizás aproximada) de una línea recta, se dice que existe una relación lineal entre las variables.
La lectura de un diagrama de dispersión se hace en base al tipo de relación entre los datos; lo fuerte o débil de la relación, la forma de la relación y la posible presencia de punto anómalos.
La relación entre los datos se denomina “correlación positiva” cuando a un aumento en el valor de la variable X le acompaña un aumento en la otra variable.
El caso inverso en el diagrama da lugar a la llamada “correlación negativa”.

El Coeficiente de Relación Lineal en los diagramas de dispersión
Además del análisis gráfico, también se ha desarrollado un indicador estadístico llamado coeficiente de correlación o “r” en los diagramas.
El valor del coeficiente de correlación lineal de Pearson (r) proporciona una medida del grado de relación entre dos variables.
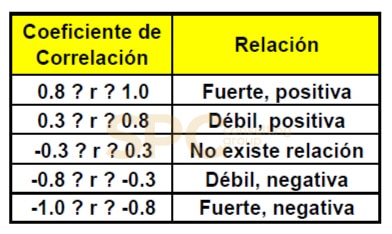
El valor del Coeficiente de Correlación es:
|r| = < 1 esto quiere decir que estará entre cero y uno.
Si r = +1 ó r = -1 se tiene entonces una correlación perfecta, lo cual significa que todos los puntos caen sobre una línea recta.
Un valor de r = 0 indicará la ausencia de relación entre las variables; entre más cercano esté el valor absoluto de r a la unidad mayor será el grado de correlación.
El coeficiente de correlación lineal de los diagramas se calcula mediante la expresión:
r = S (xy) / √(S(xx) S(yy)) donde:
S(xx) = ƩXi² – (ƩXi)² / n
S(yy) = ƩYi² – (ƩYi)² / n
S(xy) = ƩXiYi – ((ƩXi) (ƩYi)) / n
“n” es el número de parejas de datos. El término S(xy) se llama covarianza.
Ejemplo
Utilizando los datos recolectados en nuestro ejemplo, podemos hacer la siguiente tabla:

Podemos calcular el coeficiente de correlación lineal:
S(xx) = ƩXi² – (ƩXi)² / n = 295 – (43 x 43) / 8 = 63.875
S(yy) = ƩYi² – (ƩYi)² / n = 6234 – (202 x 202) / 8 = 1,1333.5
S(xy) = ƩXiYi – (ƩXi) (ƩYi) / n = 1354 – (43 x 202)/8 = 268.25
El valor del Coeficiente de Correlación es:
r = S (xy) / √(S(xx) S(yy)) = 268.25 / √(63.875)(11333.5)
r = 0.9969 La correlación es fuerte positiva.
También podemos expresarlo en términos de porcentajes por lo cual
%r = r x 100 = 99.69%.
Ejemplo 2

En la tabla se presenta que la variable X corresponde a la experiencia en semanas de cada uno de los empleados a los que se aplicó la prueba, y la variable Y al tiempo en minutos que tarda el empleado en capturar correctamente los datos de un reporte a la computadora.
El Coeficiente de Relación Lineal
S(xx) = ƩXi² – (ƩXi)² / n = 90700 / 22 – (1270)² = 17386.36
S(yy) = ƩYi² – (ƩYi)² / n = 47.77 / 22 – (28.7) ² = 10.32
S(xy) = ƩXiYi – (ƩXi) (ƩYi) / n = 1481 – (1270)(28.7) / 22 = -175.77
El valor del Coeficiente de Correlación es:
r = S (xy) / √(S(xx) S(yy)) = -175.77 / √(17386.36)(10.32)
r = – 0.415 La correlación es negativa

La Ecuación de Regresión Lineal de los diagramas de dispersión
La regresión lineal es utilizada para determinar modelos matemáticos del comportamiento y relación de dos o varias variables interrelacionadas.
El modelo que se busca corresponde a la ecuación de la “mejor” línea recta que pasa a través de los puntos. Tal ecuación, denominada Ecuación de Regresión de Mínimos Cuadrados, es, en términos de las variables X y Y, la siguiente:
Y = m x + b
m = (nƩXiYi – (ƩXi)(ƩYi))/n ƩXi² – (ƩXi)²
Esto nos dará la pendiente de la línea recta más cercana a los puntos.
b = (ƩYi – bƩXi)v/ n
Esto nos dará el punto en el cual la recta intercepta al eje x
Para nuestro ejemplo tenemos que:
La pendiente (m) = 4.67361
Intercepción (b) = 0.2299
Por ejemplo, para un valor de tiempo de 15 segundos de tiempo, ¿Cuál sería el espesor obtenido? Substituyendo:
Y (Espesor) = 4.67 x 15 + 0.2299 = 70.28 milímetros.
Conclusiones
El diagrama de dispersión es una herramienta de calidad muy útil cuando queremos conocer si hay relación entre dos variables, y nos dice gráficamente el tipo de relación o bien si los puntos están muy dispersos, que no la hay.
En ocasiones, algunos datos de los diagramas de dispersión dan lugar a puntos anómalos, que se presentan separados del patrón de puntos. El usuario debe dejar fuera del análisis esos puntos, que quizás son debidos a lecturas equivocadas o a algún cambio en las condiciones del proceso, etc.
Pero se ganará conocimiento de este último al estudiar las causas por las que se presentaron los puntos.
Un Diagrama de Dispersión no dice nada de porqué existe la correlación, por lo que es imprescindible examinar la aparente relación entre las variables desde el punto de vista científico o técnico.
Artículo por SPC Consulting Group en colaboración con el Ingeniero Gustavo Gutiérrez.
DERECHOS DE USO: Queda prohibido copiar, reproducir, distribuir, publicar, transmitir, difundir, o en cualquier modo explotar cualquier parte de este material sin la correcta atribución correspondiente o sin la autorización previa por escrito de Servicios Profesionales de Alta Consultoría S.C. (SPC Consulting Group) o de los titulares correspondientes.
Usted deberá citar este artículo copiando y pegando el siguiente texto:
Diagrama de Dispersión
SPC Consulting Group
https://spcgroup.com.mx/diagrama-de-dispersion/
Si deseas saber más sobre Diagramas de Dispersión, comunícate hoy con nosotros, o te invitamos a nuestros próximos entrenamientos en diferentes ciudades como Monterrey, Querétaro, Guadajalara, entre otras dentro y fuera de la República Mexicana y en modalidad online desde cualquier ciudad.






